La vidéo:
Version écrite!
On ne peut pas commencer cette page sans parler de la définition même de ce qu’est l’échantillonnage en astronomie.
L’échantillonnage est la portion de ciel qui est compris sur un seul pixel d’un capteur quand il est couplé à un instrument.
Cependant dites vous bien que ce n’est pas parce que l’on vous dit tel ou tel chose que vous aller améliorer vos photos ça ne donne qu’une base de travail.
Nous nous retrouvons plutôt contraint par divers éléments comme le budget ou l’impossibilité d’avoir des caméras ou instruments ayant la taille que l’on souhaite.
La valeur d’échantillonnage idéale que nous allons voir a été déterminée par des essais et des observations et
non par des calculs scientifiques qui nous auraient donnés un résultat précis.
Donc on ne fait que reprendre les chiffres d’autres personnes qui nous disent qu’ils ont eu les meilleurs résultats avec tel ou tel valeurs.
L’échantillonnage
Parlons tout de suite de la formule principale qui détermine l’échantillonnage avec une caméra et un télescope donné.
Echantillonnage = 206 x taille du pixel / Focale
L’échantillonnage: « d’arc / Pixel
Taille du pixel: µm
Focale de l’instrument: mm
L’arc seconde (« d’arc) étant une valeur d’angle. Nous observons une voute céleste circulaire donc nous exprimons les distances en degré, minute et seconde ou:
1°= 60′ (1 degré = 60 minute)
1′ = 60″ (1 minute = 60s)
Prenons un exemple celui de mon matériel de ciel profond:
Ma caméra est une ATIK 460 avec des pixels de 4.54 µm
Mon télescope est un newton qui a une focale de 800 mm
206 x 4.54 /800 = 1.17 « /pixel
Pouvoir séparateur
Parlons maintenant théorie en supposant que le ciel est totalement transparent et stable…
Chaque instrument à ce qu’on appelle un pouvoir séparateur qui correspond à sa résolution maximale, sa capacité a séparer les fins détails.
Cette valeur est aussi exprimée en « arc.
Il ne peut donc pas séparer de détails plus petits.

Son calcul s’obtient avec la formule suivante:
Ps = 120/diamètre
Qui est une formule simplifiée car le vrais calcul dépend de la longueur d’onde de la lumière mais nous nous allons utiliser la formule simplifiée qui correspond à une longueur d’onde moyenne de 120 nM
Reprenons mon télescope on obtient donc:
Ps= 120/200 = 0.6 » d’arc
Mon télescope est donc capable de séparer des détails fins de 0.6″ d’arc.
L’échantillonnage idéal
Toujours en théorie si je fais en sorte d’avoir un échantillonnage avec ma caméra qui est égal au pouvoir séparateur de mon instrument, dans notre exemple 0.6 je suis sensé être au meilleur des capacités de mon système??
Et bien non car ça voudrai dire que si j’observe une étoile qui fait 0.6″ d’arc et bien elle prendrait un seul pixel de ma caméra et serait donc carré sur ma photo.
Nous considérons donc:
Echantillonnage idéal = Ps / 2
Dans notre exemple cela fait:
0.6 / 2 = 0.3″/pixel
Pouvoir séparateur Vs SEEING
Bon tout ça c’est bien jolie mais ce n’est que la théorie en réalité le facteur qui prime avant tout, c’est les conditions de prises de vue, entre autre la turbulence atmosphérique appelée aussi le seeing exprimé en » arc.
Dans le cas ou le SEEING est supérieur à la résolution de l’instrument alors se sera lui qu’il faudra prendre en compte et c’est vrais dans la majeur partie des cas.
En France nous considérons que le seeing est généralement compris entre 1″ et 3″ de ce fait, et là je parle en Ciel profond, il ne sert à rien d’avoir un échantillonnage trop petit sous l » arc car en longues pauses nous seront obligatoirement limité par cette turbulence,
En gros un échantillonnage de 1.5 à 2″ me paraît cohérent car il faut aussi prendre en compte un facteur essentiel:
La capacité de suivit de la monture
Celle-ci doit absolument être inférieure à l’échantillonnage de votre imageur sous peine de se voir sur vos photos.
Faites très attention à ça!
Parlons maintenant Planétaire car là c’est différent.
En planétaire nous travaillons à forte focale et normalement à forte cadence d’image.
Nous arrivons plus facilement à passer au travers des périodes de fortes amplitudes de turbulence.
Ainsi nous allons plutôt rechercher l’échantillonnage idéal calculer précédemment.
On aurait tendance à vouloir sur-échantillonner pour capturer le maximum de détails au cas ou la turbulence s’arrête subitement.
En bien ce n’est pas forcément une bonne idée car ça veux dire avoir de très petits pixels moins sensibles ou alors augmenter la focale de l’instrument.
Ce qui se traduit dans les 2 cas par une augmentation du temps de pause unitaire de nos images.
Au risque de se retrouver avec une amplitude de turbulence plus élevée.
Etre sous-échantillonné au contraire nous ferait perdre la possibilité d’avoir de fins détails dans nos objets pris en photo.
Il n’y a hélas pas de secret il faut tester pour déterminer la meilleur combinaison d’instrument imageur en fonction de votre site et seul l’expérience vous le dira.
Tous ces calculs vous donnent déjà une base de travail
Autres utilisations
Une autre application de l’échantillonnage très utile est le calcul de champ apparent d’un couple instrument / caméra qui permet de déterminer si un objet entre ou pas dans la totalité du capteur.
Pour se faire c’est très simple vous prenez votre échantillonnage par exemple 1.17 en degré cela fait:
1.17/3600 = 0,000325
3600 car 1 ° = 3600 «
Que vous multipliez par le nombre de pixels en horizontal et en vertical.
Dans mon cas:
horizontal: 2750 x 0.000325 = 0.89 °
Verticale: 2200 x 0.000325 = 0.715°
Ce qui donne un champ apparent de 0.89° x 0.715° pour comparaison la lune fait 0.5 ° apparent
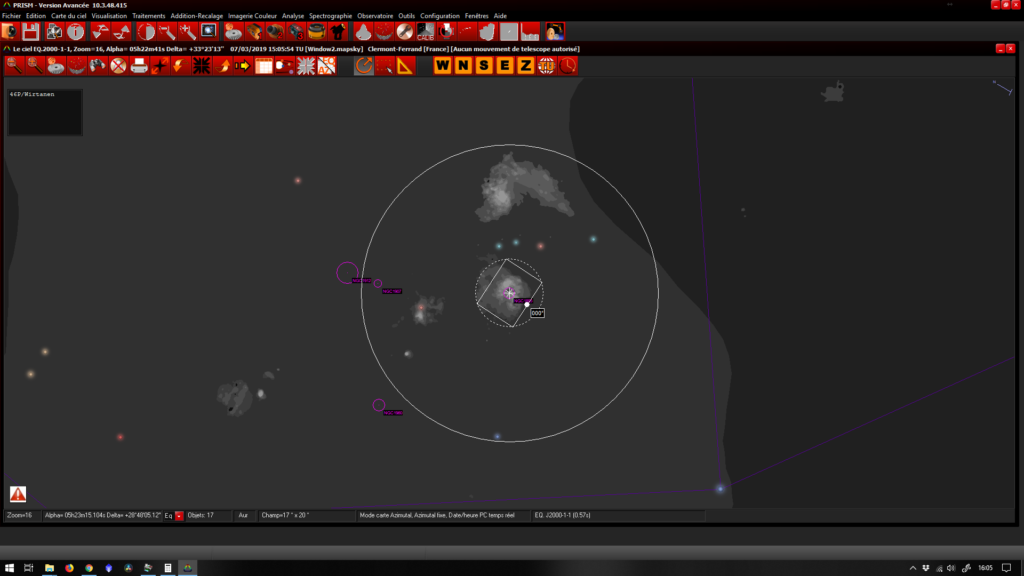
Bien entendu beaucoup de logiciels font ce calcul et vous donnent directement un aperçu du champ apparent sur une carte du ciel comme sur cette exemple avec Prism 10
Concernant les logiciels de guidage il est aussi très important de remplir les champs correspondant à la taille des pixels de la caméra de guidage ainsi que la focale de l’instrument autoguideur.
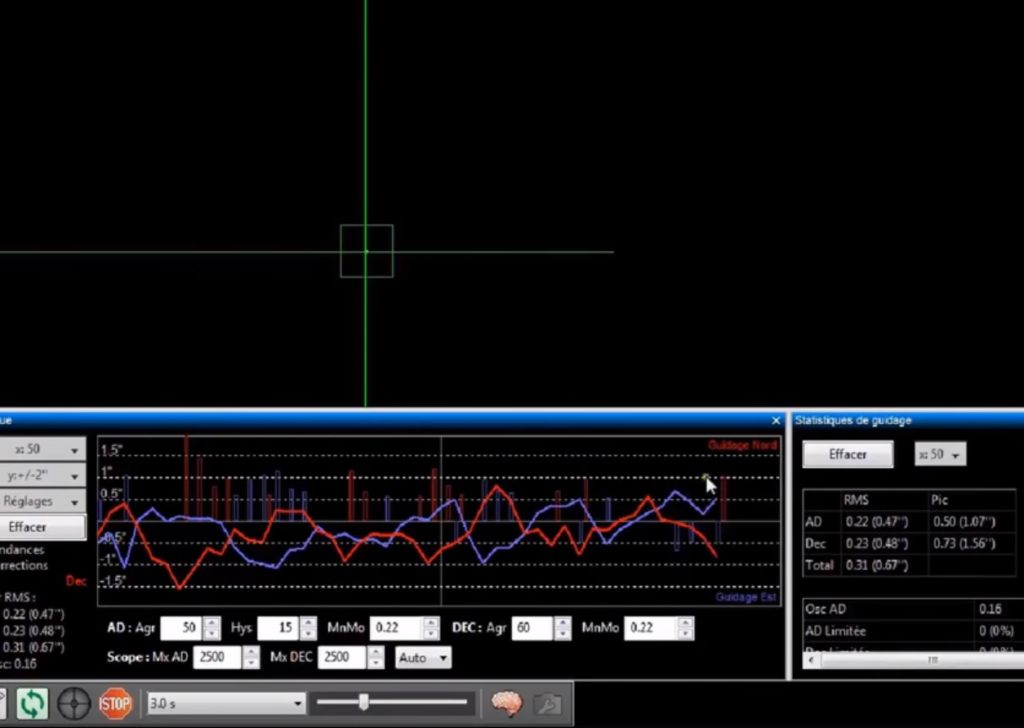
Il pourra ainsi vous présenter l’erreur de suivi en » d’arc, qui comme je vous l’ai dit doit être inférieur à l’échantillonnage de votre système imageur principale.
Pour résumer un peu tout ça:
En ciel profond essayer de rester dans un échantillonnage de 1.5 à 2.5 ou alors restez au dessus de la capacité de guidage de votre monture en gardant une petite marge.
En planétaire visez plutôt un échantillonnage = à la moitié du pouvoir séparateur de l’instrument en préférant une valeur légèrement supérieur si vous n’avez pas le choix, les valeurs inférieurs pouvant provoquer plus de soucis qu’autres choses à moins d’être dans une région ou la turbulence est plus que raisonnable!
Bonjour, je cherchai un article clair et concis. Merci pour vos explications. Une question de débutant. J’utilise une caméra planétaire CMOS ZWO ASI 290 MC color non refroidie, avec 2,13 megapixels pour des pixels de 2,9 microns de taille. J’utilise un télescope Celestron 127 SLT Nexstar avec une focale de 1500mm. L’échantillonnage est donc de 0,4″ d’arc par pixel et l’échantillonnage de 0,47″ d’arc par pixel. Comment puis-je faire varier l’échantillonnage de mon capteur caméra? Est-ce possible?
Merci pour votre aide.
Le Seul moyen de faire varier l’échantillonnage est d’ajouter une Barlow.
Merci
Bonjour,
Effectivement, il y un truc de cohérence qui me turlupine.
Si on suit le raisonnement et données de l’article, il faudrait donc une monture dont la PE < échantillonnage de l'imageur soit <1.17" arc/px.
Vous en connaissez beaucoup de montures qui, sans modification, permettent une telle précision ?
Or, la plupart arrivent à imager (plus que) correctement avec des montures dont les PE sont bien bien supérieures.
Du coup, qu'en conclure?
Merci
Bonjour
bravo pour cet article qui m’a permis de bien appréhender la chose. j’ai un nikon d5100 avec focale de 1200 donc j’en déduis que pour être à 1.5 d’échantillonnage, il faut que je réduise
la taille d’image (pixel) en la passant a moyenne. j’ai bon ?
4928 x 3264 (grande), 3696 x 2448 (moyenne), 2464 x 1632 (petite
Non ça n as rien a voir avec la résolution xpixel x xpixel mais par la taille physique d’un pixel sur le capteur.
Il existe un système sur les camera astro CCD uniquement qui permet de regrouper les pixel et donc augmenter l’échantillonnage (et par effet diminuer la taille de l’image de sortie comme vous pensez le faire avec votre APN) mais ce systeme n’existe pas sur les APN
Les APN prennent une image en pleine résolution et la redimensionne pour réduire la taille.
Techniquement, l’article est clair, bien étayé et permet de bien comprendre les différentes contraintes de l’astro photo. Bravo.
Malheureusement, au moins 32 fautes d’orthographe polluent ce beau travail et lui enlève de la crédibilité. La plupart de ces fautes ne devraient plus apparaître à la fin du CE 2 , vers 8 ou 9 ans !
Les 3/4 de ces fautes disparaîtraient en utilisant un simple correcteur d’orthographe.
Vraiment dommageable pour vos compétences !
D’accord avec vous, c’est dommage en effet, l’article perd en fluidité de lecture. Ce mal est malheureusement bien répandu sur les forums aujourd’hui.
Au passage : « 32 fautes enlèveNT de la crédibilité », si je peux me permettre !
😉
Bonjour. Les longueurs d’onde autour de 120 nm correspondent aux UVC, qui sont « très énergétiques et extrêmement dangereux pour la santé. Heureusement, ils sont totalement arrêtés par la couche d’ozone » (https://www.futura-sciences.com/sciences/definitions/physique-ultraviolet-1003/). Il serait préférable d’utiliser 550 nm, correspondant à la lumière vert-jaune.
Bonjour, vous avez parfaitement raison quant à la longueur d’onde de la lumière visible, cela m’a également interloqué.
L’article prend quelques raccourcis avec les formules (et en effet mentionne à tort la longueur d’onde moyenne de la lumière visible à 120nm au lieu de 550nm) – mais le calcul simplifié proposé par Astronote est correct.
Le calcul complet est :
1. rayon de diffraction [ρ] = 1.22 * 550 / D (en radian) = 671/D [avec 550 pour la longueur d’onde moyenne de la lumière]
2. conversion en sec d’arc : ρ* (360 / 2Pi) * 60 * 60 / 1’000’000 = 138/D
3. pouvoir séparateur théorique [PS] est 85% de ρ, donc PS = 138*85%/D = 117/D
Bref, l’approximation de 120/D est exacte 🙂
Dommage qu il y ait autant de fautes d orthographes
Le sérieux en pâtit énormément